還沒看過前一篇的大大們，建議先回去看再回來喔～

做以下的推論前，我先把等一下微積分要用到的通則寫下來：

正文開始：

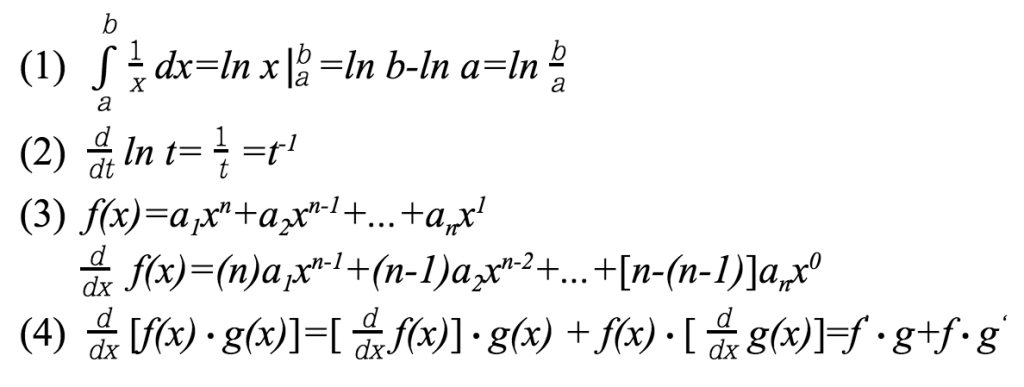
-----------以下廢文-------------

這就是「柏拉圖問題」的最基本的”標準”解答，查了一下發現很多論文也都是把中間一大串積分再用一次二次微分找到最大值 1/e (順便提一下，可不可以直接打出數學符號啊...不然截圖畫質不好又難看...)。

那我就是不太喜歡這種解法，有點不太實際。我希望直接去用窮舉的方式去把可以得到最大值的機率的 t 值給找出來。
那窮舉的工作當然就是要交給電腦來做了。不過我是一位不會程式的小渣渣，所以只好請書（再不然就交給大神爸爸和google）當我的家教拉～（拉～

因為爸爸用的是php，那我也跟隨著爸爸也一起用php來寫，看爸爸打程式的的時候都超帥的，雖然我都看不懂...爸爸都會跟我說這個東西是在幹嘛的，那個...之類的，聽下來雖然只有五成懂，但是...還是好帥啊～

-----------以上廢文--------------

首先，我就直接開始寫程式了。但爸爸跟我說在程式的最前面可以加這一串東西，可以確保搜集來的資訊是不會錯的：

if (isset($argv))
    for ($i=1;$i<count($argv);$i++)
    {
        $it = explode("=",$argv[$i]);
        $_GET[$it[0]] = $it[1];
    }

$n="\n";
$brn="<br />\n";

date_default_timezone_set("Asia/Taipei");

這是可以在終端機上直接寫上你所要的變數的參數是多少，並且設定時間用的超強的程式碼，我也就直接加在程式的最前面了。

待續...